Hollowing, i.e. Precise Geometry Preparation for 3D Print
Challenge: Geometry mesh preparation for 3D Print
The blood vessel geometry preparation for 3D print can be obtained with no arduous human work. It enables to analyse many parameters important for medical reasons, including stress or pressure distribution. Another interesting aspect is the possibility to print the vessel using special materials and place it in a physical treatment simulator. The key aspect is that the process is fully automatic to ensure that model generation for a patient does not entail any excess financial and time cost.
On the other hand, the basic requirement is to ensure the maximum precision of such a printout and, consequently, precise post-processing of the vessel mesh. One of such aspects is creating an envelope with the preset thickness which will ensure relevant mechanical properties of the obtained printout.
This apparently simple process is conditional largely on the properties of the provided vessel mesh. The mesh is usually obtained in the automatic process of CT image segmentation and may display various anomalies, e.g. vessels may be too close to one another or there may be sharp angles between the triangles.
What we did
For this reason we created an iterative algorithm resistant to most problems experienced in practice of precise geometry preparation for 3D Print. The algorithm is composed of several steps:
We create a binary mask with the preset resolution based on the preset basis of a surface mesh.
- We calculate the Euclidean Distance Transform for the area outside the vessel.
- We create the mesh for the constant distance from the vessel at the required level. In this way, we consider the possibility that the envelopes of two close vessels may touch each other automatically.
- We calculate the distance between the obtained envelope and the original vessel.
- If the distance does not meet the required tolerance, we introduce an adjustment:
a. we move vertices along the EDT gradient by a small value,
b. we relax the mesh using Laplacian smoothing,
c. if the tolerance is met, we finish the process and if not, we return to a).
Results
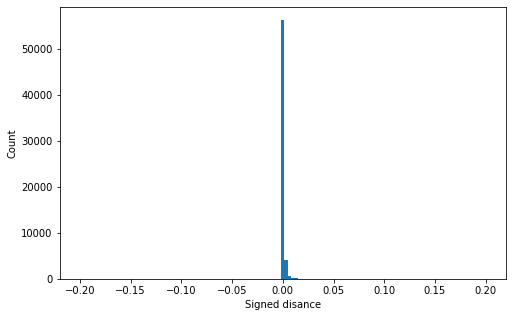
Our geometry correction reduces the error from unacceptable (Fig. 1) to the acceptable value (Fi. 2)
Error before the correction is made [mm]
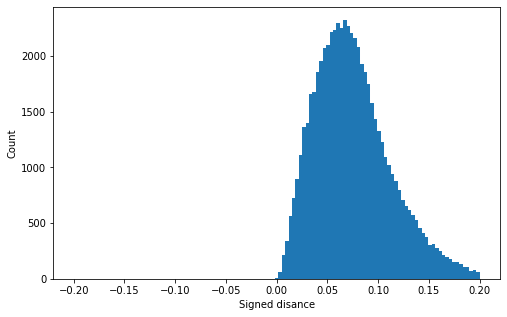
Error after the correction is made [mm]